트리
- node와 branch를 이용해서 사이클을 이루지 않도록 구성한 데이터 구조
-
트리는 항상 위에서 아래로 연결된다.
- 이진 트리 :
- 하나의 노드에서 나온 브랜치가 최대 2개인 트리
- 탐색 알고리즘 구현을 위해 많이 사용된다.
트리 기본 용어
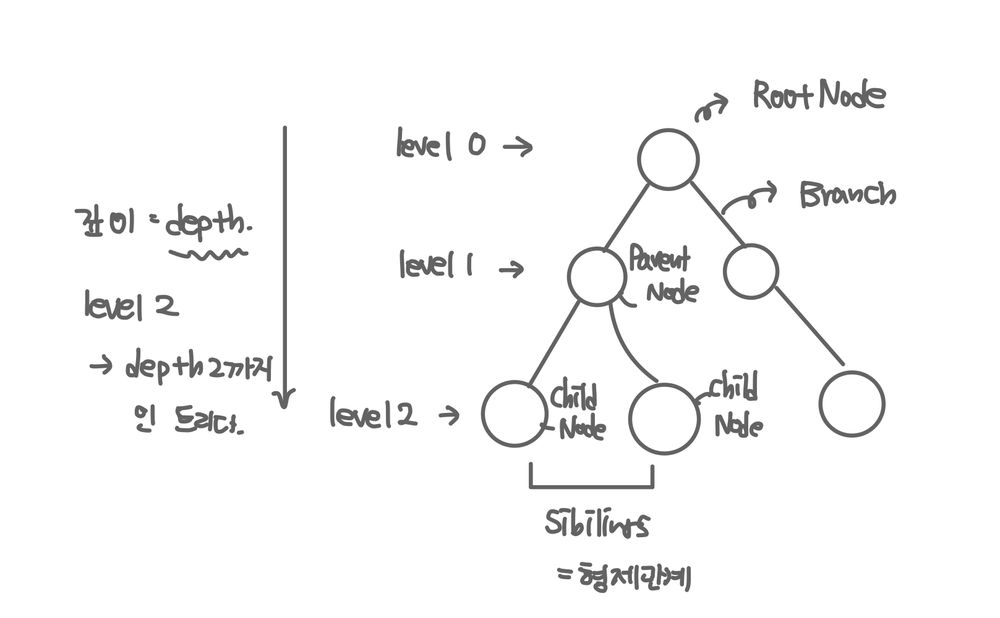
- node : 트리에서 데이터를 저장하는 기본 요소. 다른 연결된 노드에 대한 브랜치 정보를 포함한다.
- root node : 트리 맨 위에 있는 노드
- level : 최상위 노드를 level0으로 하였을 때, 하위 브랜치로 연결된 노드의 깊이를 나타냄.
- depth : 트리에서 node가 가질 수 있는 최대 level
이진 탐색 트리 (BST, Binary Search Tree)
- 이진 트리 : 노드의 최대 브랜치가 2인 트리
-
이진 트리에 조건이 추가된 트리
- 조건 : 기준 노드의 값보다 작으면 왼쪽, 크면 오른쪽에 노드를 위치시킨다.
- 탐색 속도를 개선하여 데이터 검색에 많이 사용된다.
이진 탐색 트리 구현하기
-
데이터 삽입하기
- 트리를 순회하면서 비교 대상이 되는 노드의 값과 삽입할 데이터의 값을 비교한다.
- 노드의 값보다 삽입할 데이터의 값이 크면 노드의 오른쪽 자식으로 데이터를 삽입한다.
- 노드의 오른쪽 자식이 있을 경우 자식을 비교 대상으로 설정한다.
- 다시 1번 부터 시작한다.
- 노드의 값보다 삽입할 데이터의 값이 작으면 노드의 왼쪽 자식으로 데이터를 삽입한다.
- 노드의 왼쪽 자식이 있을 경우 왼쪽 자식을 비교 대상으로 설정한다.
- 다시 1번 부터 시작한다.
fun insert(node: TreeNode) { val current = head insertNode(current, node) } private fun insertNode(current: TreeNode, target: TreeNode) { if (current.value < target.value) { current.right ?: run { current.right = target return } insertNode(current.right!!, target) } else { current.left ?: run { current.left = target return } insertNode(current.left!!, target) } } -
탐색하기 (특정 데이터가 존재하는지 확인하기)
- 비교 대상이 되는 노드의 값과 탐색할 데이터의 값을 비교한다.
- 같을 경우 true를 리턴한다.
- 값이 다를 경우 비교 대상을 다시 설정한다.
- 현재 비교 대상이 되는 노드보다 탐색할 데이터의 값이 크다면 비교 대상이 될 노드를 현재 비교 대상 노드의 오른쪽 자식으로 설정한다.
- 현재 비교 대상이 되는 노드보다 탐색할 데이터의 값이 작다면 비교 대상이 될 노드를 현재 비교 대상 노드의 왼쪽 자식으로 설정한다.
- 1번 부터 반복한다.
- 비교 대상이 없는 경우 false를 리턴한다.
fun search(value: Int): Boolean { val current = head return searchTreeNode(current, value) != null } private fun searchTreeNode(current: TreeNode, target: Int): TreeNode? { if (current.value == target) { return current } var next: TreeNode? = null next = when { current.value < target -> current.right ?: return null else -> current.left ?: return null } return searchTreeNode(next, target) } -
데이터 삭제하기
- 삭제되는 경우의 수를 생각
- 자식이 없는 노드를 삭제하는 경우
- 자식이 1개 있는 노드를 삭제하는 경우
- 자식이 2개 있는 노드를 삭제하는 경우
- 구현
- 삭제 대상이 되는 노드를 찾는다.
-
삭제 대상이 되는 노드가
- 자식이 없는 노드이고
- 삭제 대상 노드가 부모 노드의 오른쪽 노드일 경우 부모의 오른쪽 노드의 값을 null로 설정한다.
- 삭제 대상 노드가 부모 노드의 왼쪽 노드일 경우 부모의 왼쪽 노드의 값을 null로 설정한다.
- 자식이 1개 있는 노드일 경우
- 삭제 대상 노드가 부모 노드의 오른쪽 노드일 경우 부모의 오른쪽 노드의 값을 존재하는 자식의 값으로 설정한다.
- 삭제 대상 노드가 부모 노드의 왼쪽 노드일 경우 부모의 왼쪽 노드의 값을 존재하는 자식의 값으로 설정한다.
- 자식이 2개 있는 노드일 경우
-
삭제 대상 노드가 부모 노드의 왼쪽 노드이고,
- 삭제 대상 노드의 오른쪽 자식중 가장 작은 값을 가진 노드(selected)의 자식이 없을 경우 selected노드를 삭제 대상 노드의 위치로 옮긴다.
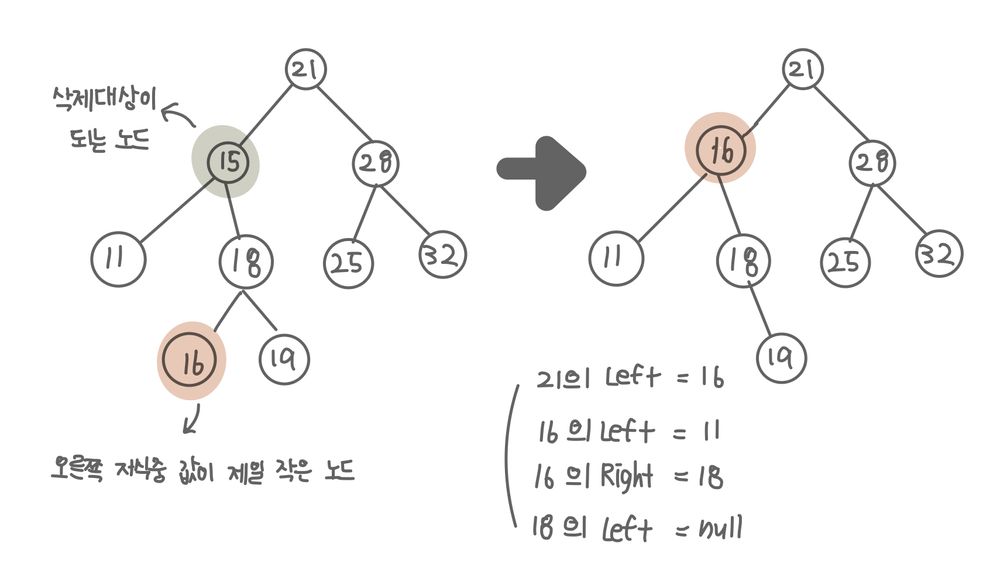
- 삭제 대상 노드의 오른쪽 자식중 가장 작은 값을 가진 노드(selected)의 오른쪽 자식이 있을 경우 selected노드를 삭제 대상 노드의 위치로 옮기고, selected노드의 오른쪽 자식을 selected의 부모 노드의 왼쪽 자식으로 설정한다.
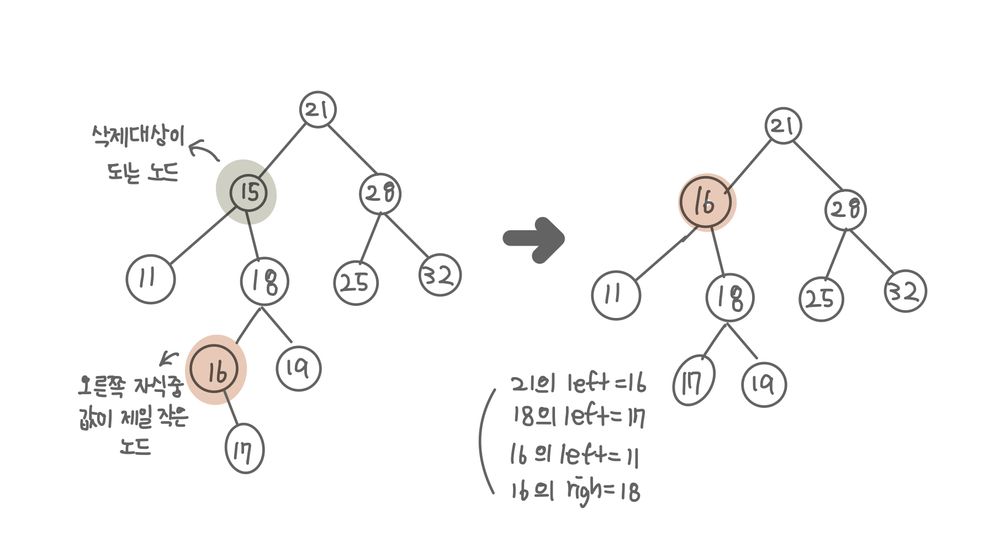
- 삭제 대상 노드의 오른쪽 자식중 가장 작은 값을 가진 노드(selected)의 자식이 없을 경우 selected노드를 삭제 대상 노드의 위치로 옮긴다.
- 오른쪽 위와 반대로.
fun delete(value: Int): Boolean { val current = head val result = searchWithParent(current, current, TreeNode(value)) if (result.isEmpty()) { return false } val (parent, deleted) = result // 1. 삭제할 노드가 leaf노드인 경우 if (deleted.left == null && deleted.right == null) { when { parent.value < deleted.value -> parent.right = null else -> parent.left = null } return true } // 2. 삭제할 노드의 자식 노드가 1개인 경우 if (deleted.left == null || deleted.right == null) { val node = if (deleted.right == null) deleted.left else deleted.right when { parent.value < deleted.value -> parent.right = node else -> parent.left = node } return true } // 3. 삭제할 노드의 자식노드가 2개인 경우 val (parentOfSelected, selected) = findMin(deleted.right!!, deleted.right!!) if (selected.right != null) { parentOfSelected.left = selected.right } else { parentOfSelected.left = null } when { parent.value < deleted.value -> parent.right = selected else -> parent.left = selected } selected.left = deleted.left selected.right = deleted.right return true } private fun findMin(parent: TreeNode, current: TreeNode): List<TreeNode> { if (current.left == null) { return listOf(parent, current) } return findMin(current, current.left!!) } private fun searchWithParent(parent: TreeNode = head, current: TreeNode = head, target: TreeNode): List<TreeNode> { if (current.value == target.value) { return listOf(parent, current) } val next = when { current.value < target.value -> current.right ?: run { return emptyList() } else -> current.left ?: run { return emptyList() } } return searchWithParent(current, next, target) }