[알고리즘] 그래프 탐색 알고리즘2 - 최단 경로 알고리즘

최단 경로 알고리즘

최단 경로 문제

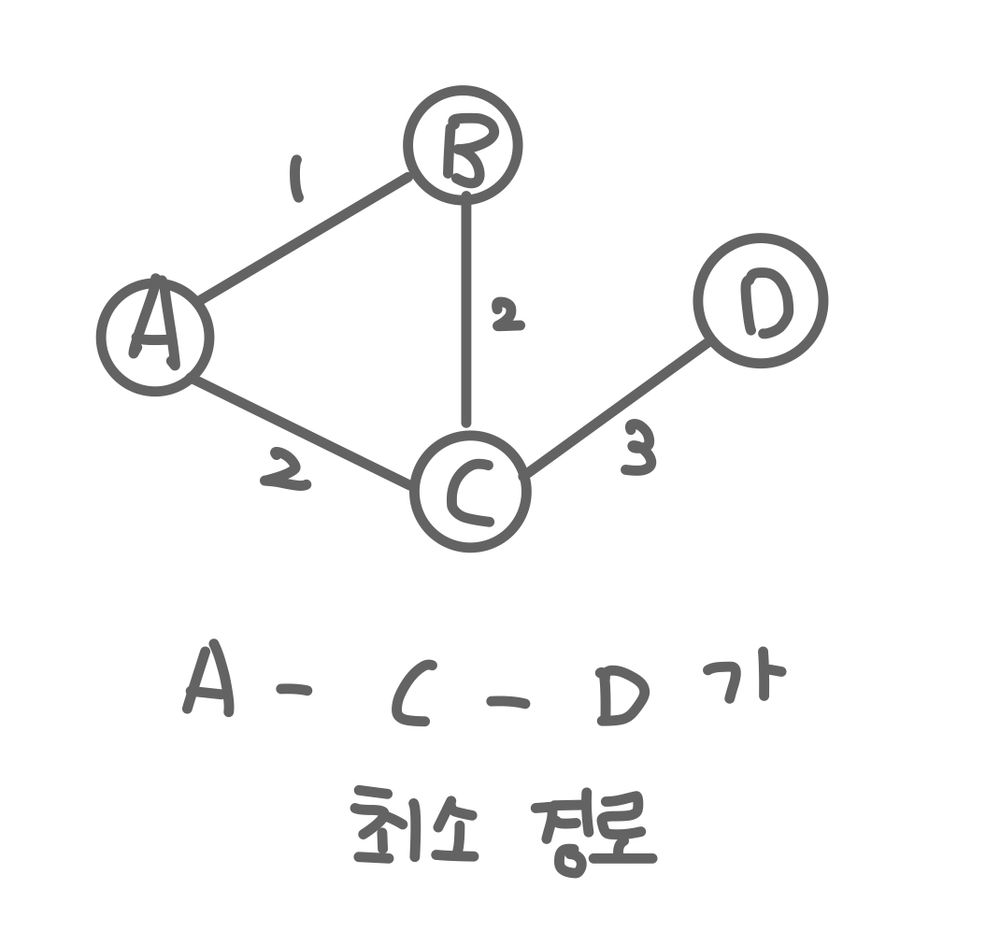
두 노드를 잇는 가장 짧은 경로를 찾는 문제
가중치 그래프에서 간선의 가중치 합이 최소가 되도록 하는 경로를 찾는 것이 목적
최단 경로 문제의 종류
1. 단일 출발, 단일 도착 최단 경로 문제 : 특정 노드 U에서 출발, 또 다른 노드 특정 노드 V에 도착하는 가장 짧은 경로를 찾는 문제
2. 단일 출발 최단 경로 문제 : 특정 노드 U와 그래프 내 다른 모든 노드 각각의 가장 짧은 경로를 찾는 문제
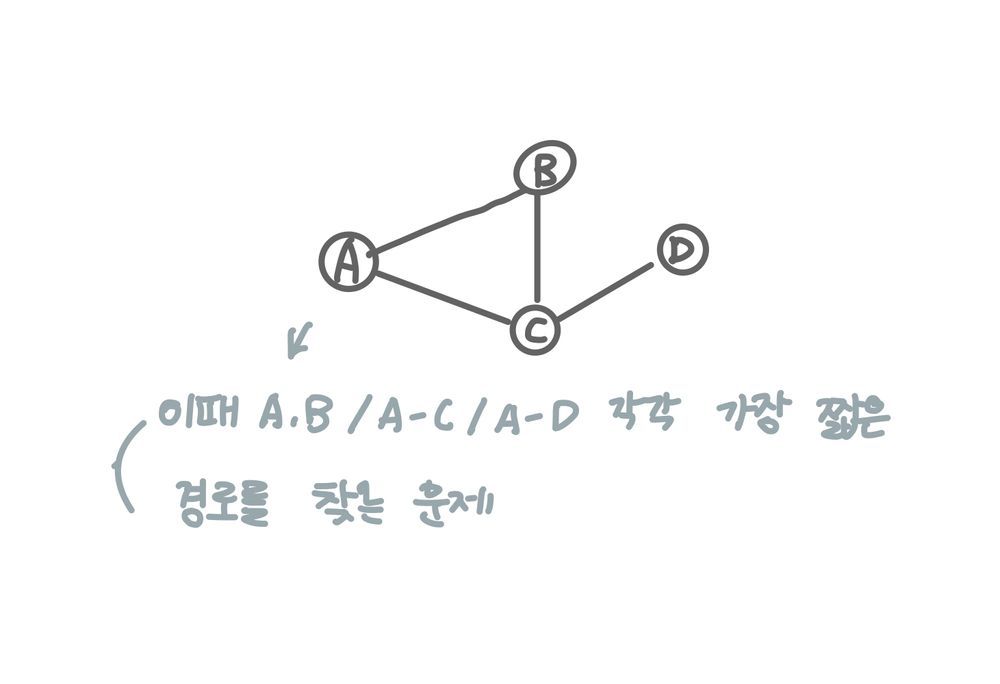
3. 전체 쌍 최단 경로 문제 : 그래프 내의 모든 노드 쌍(U,V)에 대한 최단 경로를 찾는 문제

최단 경로 알고리즘 - 다익스트라 알고리즘

최단 경로 문제 종류 중 2번에 해당하는 문제를 해결하는 알고리즘
첫 정점을 기준으로 연결되어 있는 정점들을 추가해 가면서 최단 거리를 갱신하는 기법(bfs와 유사)
- 첫 정점의 인접 노드 간의 거리부터 계산.
우선 순위 큐를 사용함
- 현재 가장 짧은 거리를 항상 먼저 꺼내기 때문에 계산 양을 줄일 수 있다.
첫 정점을 기준으로 배열을 선어하여 첫 정점에서 각 정점까지의 거리를 저장.
- 초기에 첫 정점의 거리는 0, 나머지는 무한으로 설정
- 우선 순위 큐에 첫 정점을 먼저 넣는다.
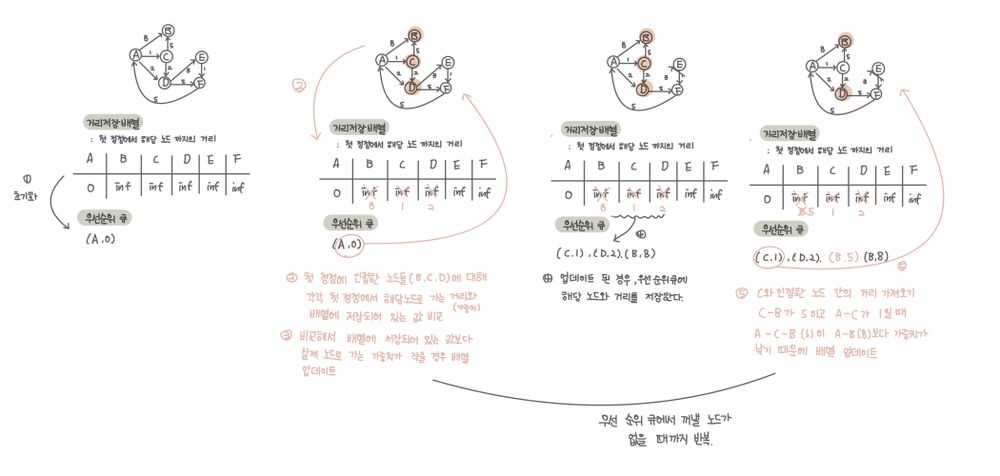
우선순위 큐에서 노드를 꺼낸다. (처음에는 첫 정점이 꺼내짐.)
- 첫 정점에 인접한 노드들에 대해 첫 정점에서 각 노드로 가는 거리와 현재 배열에 저장되어 있는 첫 정점에서 각 정점까지의 거리를 비교
- 배열에 저장되어 있는 거리보다 첫 정점에서 해당 노드로 가는 거리가 더 짧을 경우 배열에 해당 노드의 거리를 업데이트한다.
- 배열에 해당 노드의 거리가 업데이트 된 경우, 우선 순위 큐에 넣는다.
- 결과적으로 너비 우선 탐색과 유사하게 첫 정점에 인접한 노드들을 순차적으로 방문하게 된다.
- 거리가 먼 노드들은 우선 순위가 낮아짐.
2번의 과정을 우선 순위 큐에서 꺼낼 노드가 없을 때까지 반복.

dijkstra

    fun main() {
        val graph = mapOf(
            'A' to mapOf('B' to 8, 'C' to 1, 'D' to 2),
            'B' to mapOf(),
            'C' to mapOf('B' to 5, 'D' to 2),
            'D' to mapOf('E' to 3, 'F' to 5),
            'E' to mapOf('F' to 1),
            'F' to mapOf('A' to 5),
        )

        val queue = PriorityQueue<Pair<Char, Int>>(compareBy { it.second }).apply {
            add(Pair('A', 0))
        }


        val distanceArray = mutableMapOf(
            'A' to 0,
            'B' to Int.MAX_VALUE,
            'C' to Int.MAX_VALUE,
            'D' to Int.MAX_VALUE,
            'E' to Int.MAX_VALUE,
            'F' to Int.MAX_VALUE,
        )

        println(dijkstra(distanceArray, queue, graph))


    }

    fun dijkstra(
        distanceArray: MutableMap<Char, Int>,
        priorityQueue: PriorityQueue<Pair<Char, Int>>,
        graph: Map<Char, Map<Char, Int>>
    ): MutableMap<Char, Int> {

        if (priorityQueue.isEmpty()) {
            return distanceArray
        }

        val (currentNode, currentDistance) = priorityQueue.poll()

        graph[currentNode]?.forEach {
            val distance = currentDistance + it.value

            if ((distanceArray[it.key] ?: 0) > distance) {
                distanceArray[it.key] = distance
                priorityQueue.add(Pair(it.key, distance))
            }

        }

        return dijkstra(distanceArray, priorityQueue, graph)
    }